Soal Pembahasan Gerak Parabola Fisika SMA

Dear all

Di Website Senopati Education Center saat ini telah di buka kursus online untuk Sekolah Menengah Atas (SMA). Walaupun sistem Ujian Nasional akan digantikan konsepnya pada tahunn 2021, namun sepertinya tidak akan banyak menghilangkan materi yang ada sebelumnya. Kita mulai dari Gerak Parabola. Materi ini adalah pengembangan dari Gerak Lurus Beraturan (GLBB) dan Gerak Berubah Beraturan (GLBB) pada waktu kita dibangku Sekolah Menengah Pertama (SMP).

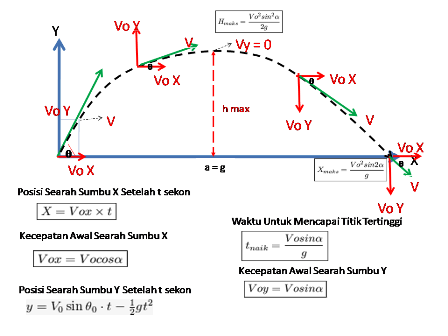
Seperti pada gambar, jika biasanya kita  mencari kecepatan pada arah mendatar (sumbu x ) atau hanya jarak vertikal (Sumbu Y)

• (X = Vo .t),
• Vt = Vo.t + a.t
• Perpindahan benda pada saat t (waktu),  yaitu       X = Vo.t + 1/2 a.t kuadrat
• Vt kuadrat = Vo kuadrat + 2. a.s
• atau gerak jatuh bebas pada arah vertikal (sumbu Y) seperti h = 1/2 g.t  kuadrat , Vt = g. t
•  gerak vertikal keatas seperti  Vt = Vo – g.t
• Vt kuadrat = Vo kuadrat – 2. g h
• h = Vo.t – 1/2 g.t kuadrat
• t naik = Vo / g  , h max = Vo kuadrat / 2.g

 

Maka di gerak Parabola rumus-rumus diatas (GLB, GLBB, Gerak jatuh bebas serta gerak vertikal keatas ) tidak akan jauh berbeda, hanya saja di gerak parabola ini kita akan mencari kecepatan dan komponen-komponen  di  arah melengkung (membentuk sebuah sudut). Seperti ketika menendang bola, maka akan terbentuk lintasan yang seperti parabola, kita bisa mencari kecepatan yang ada pada titik tertentu di sepanjang lintasan itu (lihat gambar). Nah untuk mencarinya maka kita akan butuh komponen pada sumbu x dan sumbu y. Pada sumbu x berlaku cosinus untuk sudutnya dan di sumbu Y sinus (lihat gambar). Sehingga untuk mencari kecepatan ataupun sudutnya nantinya bisa dirumuskan sebagai

Supaya kalian tidak bingung kita langsung ke Contoh soal dan Pembahasannya dari yang paling sederhana saja ya, check it out :

pada setiap benda yang bergerak dengan lintasan parabola, komponen kecepatan menurut sumbu x (mendatar) dan komponen kecepatan menurut sumbu y (tegak) berlaku . . . . . .

Pembahasan = Seperti pada gambar diatas, maka

• Kecepatan gerakan parabola pada sumbu x konstan dan memenuhi persamaan  Vx = V cos θ x t
• sedangkan pada sumbu y adalah GLBB dan memenuhi Vy = v sin θ -gt kuadrat

Sebuah bola ditendang dengan sudut elevasi 45 derajat, dengan kecepatan awal 10 m/s. Jika percepatan gravitasi 10 m/s2, maka lamanya bola diudara adalah. . . . . . .

Pembahasan  =Waktu Maksimum ada pada GERAK VERTIKAL

Diketahui:
θ = 45°
vo = 10 m/s
g = 10 m/s²

ditanya = tmax?

Jawaban :
tmax = voy / g
tmax = vo sin 45° / g
tmax = 10 . 1/2√2 / 10
tmax = 1/2√2 sekon

Cahyani melempar bola basket ke lapangan dengan sudut elevasi 0, dan kecepatan awal V. Jika percepatan gravitasi Bumi g, maka waktu yang diperlukan untuk mencapai titik tertinggi adalah ….

Pembahasan =
Diketahui:
sudut elevasi = θ
kecepatan awal = vo
percepatan gravitasi = g

Ditanyakan:
waktu mencapai titik tertinggi (t)

Jawab =  Pada saat di titik tertinggi kecepatan komponen vertikal bernilai nol, sehingga

Vty = Voy – sin gt
0 = Voy – gt
t = Voy / gt

Maka
t = Voy sin θ / g

Sebuah peluru ditembakkan dari ujung senapan yang membentuk sudut kemiringan 30° terhadap tanah. jika kecepatan awal peluru 50 m/s dan  percepatan gravitasi 10m/s2  maka waktu yang diperlukan untuk mencapai titik  tertinggi adalah . . . . .

Pembahasan =

Diketahui
Vo = 50 m/s
α = 30°
g = 10 m/s²

Ditanya  adalah t (Tertinggi) = ?

Jawab

t max = Vo sin θ / g

= (50 m/s x sin 30 ) / 10 m/s2

= (50 x ½) / 10

= 2,5 sekon

Sebuah bola golf dipukul dengan sudut kemiringan 37 derajat terhadap permukaan tanah, dengan kecepatan awal 40 m/s. kecepatan bola golf pada saat berada di titik tertinggi adalah …

Pembahasan =

Diketahui :
sudut = 37 derajat
V0 = 40 m/s

ditanya : kecepatan saat di titik tertinggi

di titik tertinggi, Vy = 0 (Lihat gambar) 

Dari rumus  V = akar(Vx^2 + Vy^2)

Maka
V = akar(Vx^2)
V = Vx
Vx = V0 . cos θ = 40 . 0,8 = 32 m/s

Sebuah bola ditendang dengan kecepatan awal 20m/s bola tersebut jatuh ditengah lapangan yang berjarak 40m dari kaki penendang. jika percepatan gravitasi bumi 9,8m/s², maka sudut elevasi bola pada saat ditendang terhadap permukaan tanah adalah . . .

Pembahasan =

Diketahui
Vo = 20 m/s
X max = 40 m
g = 9,8 m/s kuadrat

Ditanya = Sudut elevasi saat bola ditendang ?

Karena waktu belum diketahui, maka kita cari dengan membuat persamaan dari kedua sumbu, yaitu

X = Vo cos θ . t
40 = 20 cos θ . t  (persamaan 1 )

Y = Vo sin θ – gt
0 = 20 sin θ – 9,8 t
t = (20/9,8) sin θ
t = 2,04 sin θ (Persamaan 2)

Harus diingat bahwa waktu sampai titik maksimum (sumbu x ) dua kali titik tertinggi, maka persamaan 2 menjadi    t = 4,08 sin θ (Persamaan 2)

Kita subtitusi persamaan 1 dan 2

40 = 20 cos θ . t
40 = 20 cos θ . 4,08 sin θ
40 = 10 x 4,08 x 2 sin θ cos θ   {keterangan : 2 sin θ cos θ menjadi sin (2 θ) }
40 = 10 x 4,08 sin (2 θ)
40 = 40,8 sin (2 θ)
Sin (2 θ) = 0,98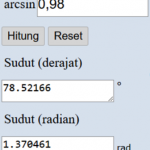

arcsin 0,98 = 78.52
78.52 /2 = 39,26

Maka sudut elevasi = 39,26 derajat

 

 

Sandi menendang sebuah bola bermassa m dengan kecepatan awal v dari puncak sebuah tebing yang memiliki ketinggian h. Jika percepatan gravitasi bumi = g ,  maka komponenyang tidak mempengaruhi jarak horisontal yang ditempuh bola adalah

Pembahasan =

Jarak horisontal maksimum (x max) dapat kita cari dari :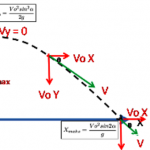

Xmax = ( 2Vo² sin θ cos θ ) / g

Maka dari sini ketinggian tebingnya tidak mempengaruhi dalam pencarian jarak horisontal

 

 

Seorang anak berdiri di teras lantai dua sebuah gedung. Kedua tangan anak tersebut memegang kelereng. Kemudian dilemparkan dalam arah mendatar. Kelereng dari tangan sebelah kiri dilemparkan dengan kecepatan V, sedangkan sebelah kanan dengan kecepatan 1/4 V. Pernyataan berikut yang benar adalah :

Pembahasan =

Vt = Vo + a x t
Vt = Vo + a.t
a. t = Vt – Vo
a = ( Vt -Vo) /t    . . . Persamaan 1

Vt = Vo + a x t
Vt = ¼ Vo + a.t
a. t = Vt – ¼ Vo
a = ( Vt -1/4 Vo) /t  . . . Persamaan 2

Lalu bandingkan kedua persamaan diatas

( Vt -Vo) /t = ( Vt -1/4 Vo) /t

Maka

-Vo = -1/4 Vo

Kelereng dengan kecepatan V memiliki percepatan lebih kecil dari kecepatan ¼ V

Seorang atlet panahan menembakkan panahnya dengan sudut elevasi O terhadap arah mendatar dengan kecepatan awal 18 m/s. Panah tersebut mengenai sasaran yang berjarak 16,2 meter dari pemanah. Jika g = 10 m/s?, maka sudut elevasi yang  dibentuk anah panah terhadap permukaan tanah adalah ….

Pembahasan =

Diketahui:
sudut elevasi = θ
kecepatan awal = 18 m/s
percepatan gravitasi = 10 m/s2
Jarak ( x ) = 16,2 meter

Ditanyakan:
sudut elevasi (θ) terhadap permukaan tanah ?

Jawab

Karena waktu belum diketahui maka kita buat dalam bentuk persamaan terdahulu

 

X = Vo cos θ.t
16,2 = 18 cos θ .t  (persamaan 1)

Y = Vo sin θ – gt
0 = 18 sin θ – 10 t
t = 1,8 sin θ (persamaan 2)

Ingat bahwa waktu sampai titik maksimum dua kali titik tertinggi, maka persamaan 2 menjadi t=3,6 sin θ

lalu kita gabung persamaan diatas menjadi

16,2=18 cos θ t
16,2=18 cos θ x 3,6 sin θ
16,2=9 x 3,6 x 2 sin θ cos θ
16,2=9 x 3,6 sin(2θ)
sin(2θ)= 16,2/ 32,4
Sin (2θ) = 0,5
2θ=30 (arcsin 0,5 = 30)
a=15 derajat

Sebuah bola kasti dipukul dengan kecepatan awal 20 m/s dan membentuk sudut 60 derajat terhadap permukaan tanah ( g= 10m/s2). Tinggi maksimum yang dapat dicapai bola kasti adalah . . . .

Pembahasan =

Diketahui:
sudut elevasi (θ) = 60 derajat
kecepatan awal = 20 m/s
percepatan gravitasi = 10 m/s kuadrat

Ditanyakan:
Tinggi maksimum (Y max) ?    Y max = ( Vo² sin² θ ) / 2g

Langsung saja kita masukan angkanya ke rumus Y max diatas

= {20 kuadrat x Sin² 60° } / 2 (10)
= {400 x (sin 60° × sin 60°)}/ 20
= {400 x (½√3 × ½√3)} / 20
= (400 x ¾) / 20
= 300 / 20
= 15 meter

Oke guys, ini baru soal yang paling sederhana untuk membantu kalian memahami materi tentang gerak parabola ini. Jika ada pertanyaan, atau soal yang kalian tidak mengerti bisa ditanyakan ke kolom komentar.  Kalau mau belajar si Kelas Online Senopati Center secara rutin, kalian tinggal hubungi hotline kami. Ingat bahwa kami menyediakan Kelas Online dengan sistem Live Video chat dan Live Chat, jadi disini kalian langsung bertatap muka atau berhubungan dengan guru kami.

Sampai jumpa 😉